“初探小学数学新课程标准”讲稿
泸县方洞镇雨坛中心小学校 罗勇
2001年:《全日制义务教育数学课程标准(实验稿)》
2011年:《全日制义务教育数学课程标准(修改稿)》
2022年,义务教育数学课程标准,再次大修,也让我们一线数学教师再次关注。
1、四个领域: 数与代数,图形与几何,统计与概率, 综合与实践。
2、 主要的关键词:
数 感,符号意识 ,空间观念 ,几何直观, 运算能力,模型思想 , 推理能力,数据分析观念, 应用意识,创新意识。
说一说前面五个方面:数感,符号意识,空间观念,几何直观,运算能力 。
3、先来看看体现课程理念的两句话:
第①句“人人都能获得良好的数学教育。”要求我们一线教师高标准备课,高效率教学。
第②句“不同的人在数学上得到不同的发展。”要求我们教师针对学生个性差异,以特别的标准,让学生都能稳步提升,得到良好发展。
第一部分 数感
数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟。
建立数感有助于学生理解现实生活中数的意义,理解或表述具体情境中的数量关系。
如同歌手的乐感一样…… 做到心中有数。
简单、通俗地说,数感就是数的感觉。
教学数数、数的基数意义与序数意义、数序与数的大小比较……都有助于形成数感。
3000006000 读作: 三十亿零六千
30600 读作: 三万零六百
30060 读作: 三万零六十
30006 读作: 三万零六 读出数感!
6789读作( 六)千 (七 ) 百 ( 八) 十 ( 九 )
6789由( 6 )个千,( 7 )个百,( 8 )个十和 ( 9 )个一组成.
6789=( 6 )×1000+ ( 7 )×100+ ( 8)×10+( 9 )
1.在数的概念教学中培养数感
先看动画。
数的感觉,一下就有了。
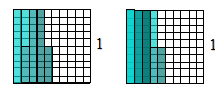
小数乘法计算法则推导:
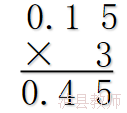
再看图示,把单位“1”平分成100份,先取15份,再取15份,再取15份,得到45份,就是0.45.
或 把单位“1”,平分成10份,先取3个1份,再把这单位“1”细分成100份,依次取3个5份,最后得到100份中的45份,也就是0.45.
竖式计算,或图示表达,图形结合,真正诠释了这个数,同时让学生深刻认识了此类数。
3.在解决实际问题中展现数感
72×15=1080(米)
1080稍大于1000;
1080超过2000的一半,都是真正的数感。
不管是图示表达,还是数字的比较,都体现了真正的数感。
第二部分 符号意识
符号意识主要是指能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性。
建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式。
对于小学数学来说:平时教学中,多使用一些符号,
首先让学生从小亲近符号,接受、理解符号!
对学生中学学习有很大意义,你的学生会感激你。
例如:运算符号 + - × ÷ 多么形象,多么直观啊。
又如:关系符号 = > <
“再也没有比平行而又等长的短线段更确切的相等符号了” ——列科尔德(英国)
诸如此类,举不胜举。
可见:数学符号如同“象形文字”,简洁、生动、形象、传神。
符号本身就具有促进理解,帮助记忆的教学功能。让数学符号帮助我们教学。
任何教学艺术、任何语言描绘,都相形见绌!
其次是让学生感悟符号表达的优势与作用。

再看,把结果乘3减21。告诉我计算结果,我立即能判断出你想的整数是多少?
设:所想的数为x。
则 ( 2x+7 )×3-21
=6x+21-21
=6x
这就是数学符号的魔力,数学符号的神奇。
第三部分 空间观念
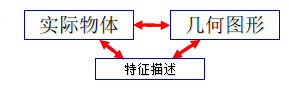
空间观念主要是指根据物体特征抽象出几何图形,根据几何图形想象出所描述的实际物体;想象出物体的方位和相互之间的位置关系;描述图形的运动和变化;依据语言的描述画出图形等。
由此可见:两者之间的可逆关系
空间观念发展规律
↓
空间观念(表象的形成)
↓
空间想象(表象的改造)
三种水平既递进发展,又交错共存。
小学生空间观念发展的若干特点
(1)从感知强成份到感知弱成份

如:形状 边的长短是强成份;
关系 角的大小是弱成份。
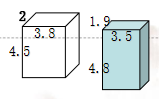
一个包装盒,如果从里面长3.8分米,宽2分米,容积是34.2立方分米。小胖想用它来装一件长3.5分米,宽1.9分米,高4.8分米的礼物,是否装得下?
3.5×1.9×4.8=31.92
34.2÷3.8÷2=4.5
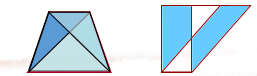
(4)从直观辨认图形到语言描述特征
如:识别梯形→说出梯形特征
(5)从使用日常语言到使用几何语言
如:底面→横截面
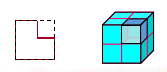
(6)从形成二维空间观念到三维空间观念
又 怎样发展学生的空间观念?
(1)观察:有序观察,选择对象,变换角度;
(2)操作:学会画图,动手操作,自我释疑;
(3)变式:变化形状,变化位置,变化大小;
(4)辨析:同中见异,异中求同,精确分化;
(5)结合:形象与语言结合,数与形结合。
第四部分 几何直观
几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。
几何直观可以帮助学生直观地理解数学,在整个数学学习过程中都发挥着重要作用。
案例1:团体操原来队伍每行10人,有5行。现在调整成每行增加3人,增加2行,现在需要增加多少人?
第五部分 运算能力
主要是指能够根据法则和运算律正确地进行运算的能力。
培养运算能力有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题。
合理选择算法正确运算

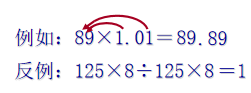
老师们,本次讲座到此结束了,不当之处,请批评指正,感谢。


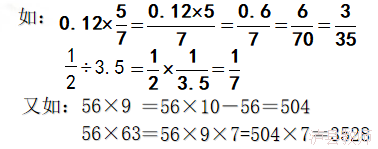

账号+密码登录
手机+密码登录
微信扫码登录
还没有账号?
立即注册