2023.10.13CCtalk 教学设计《多边形面积整理复习》（徐红琴）

姓名：

徐红琴

工作单位：

泸县玄滩镇学校

学科年级：

五年级

教材版本：

西师版

一、教学内容分析

   本节课的教学内容是五年级多边形的面积整理与复习。进一步巩固多边形面积公式，及灵活运用。学习的基本思路是学生运用转化的数学方法将组合图形转化为基本熟悉的图形进行计算，进一步鼓励学生一题多解，培养学生的发散思维和创新精神。

二、教学目标

知识与技能：使学生进一步理解并掌握平行四边形、三角形和梯形的面积公式，能灵活应用公式解决组合图形的面积。

过程与方法：引导学生回忆、讨论与交流，沟通“多边形面积”知识间的内在联系，从而进行系统地整理与复习。

情感态度与价值观：在复习整理的过程中，使学生感悟“转化”思想，发展空间想象能力，养成自己整理所学知识的意识和良好学习习惯。

三、教学策略选择与设计

  本节课的设计理念是让学生巧妙运用转化的数学思想，通过迁移，由形象直观自然过渡到抽象理解。教学中教师主要采用的方法是复习回顾、归纳总结、迁移推理，让学生通过观察发现、讨论交流，学以致用。

四、教学重点及难点

  教学重点：熟练计算平行四边形、三角形、梯形及组合图形的面积，体会转化的数学思想。

  教学难点：多边形面积公式之间的内在联系。

五、教学过程

教师活动

预设学生活动

设计意图

  一、回忆旧知，导入课题

1.这学期我们学过哪些平面图形的面积？

2.你能归纳整理出来公式来吗？

3.板书课题：

   多边形的面积整理与复习

1.学生可能说出长方形、正方形、平行四边形、三角形、梯形等。

2.学生说出图形的面积公式，但对于推到过程可能还有点模糊，需要进一步明理。

启发学生回忆学过的知识，使头脑重现表象，建立空间观念，为复习做好准备，使教学活动建立在学生认知发展水平和已有知识经验基础之上。

   二 、梳理知识，形成体系

（一）你能说一说这些平面图形的面积公式是如何推导出来的吗？

1．观看动画（各图形公式推导过程）

2.学生小组内讨论、叙述推导过程。

3.学生汇报交流，及时评价、引导。

（二）师生共同完善知识结构

1.（出示平行四边形），把平行四边形转化成长方形，由长方形的面积S=ab推导出S=ah。

2.（出示三角形），把三角形转化成平行四边形（或长方形），由平行四边形面积S=ah（或长方形面积S=ab）推导出S= ah÷2。

3.（出示梯形），把梯形转化成平行四边形（或三角形）由平行四边形面积S=ah（或三角形面积S= ah÷2）推导出S=（a+b）h÷2。

4.强调除以2的意义，提示学生计算时不要忘记除以2。

5.渗透“转化”的学习思想和方法。

6.让学生知道面积底或高，求高或底的方法。特别是求三角形和梯形底或高时首先要用面积乘2，让学生明白要先把三角形或梯形转换成平行四边行。

1.学生通过相互交流讨论，小组内整理记录梳理知识。

2.小组内交流讨论每个图形面积的推到过程。

3.结合大屏幕演示，进一步交流多边形的面积推导过程以及面积公式，尤其是三角形和梯形中的除以2。

通过回忆整理，向学生提供充分从事数学活动的机会，帮助他们在自主探索与合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得必要的数学活动经验。

三、综合运用

   同学们对这些图形面积计算公式非常熟练了，但是是否真正理解了呢？老师要考考大家

1.计算图形面积

（1）学生独立完成练习单。

（2）集体订正（学生汇报交流）。

2.小法官，巧判断。

（1）平行四边形的底越长，它的面积就越大。（     ）

（2）三角形面积等于与它等底等高平行四边形面积的一半。（     ）

（3）面积相等的两个梯形一定能拼成一个平行四边形。（     ）

（4）等底等高的两个三角形面积相等。（     ）  

（5）把一个长方形的木条框拉成一个平行四边形，它的周长和面积都不变。（     ）     3

1.判断中学生各抒己见，交流自己的看法。

2.有的学生只能判断对错，但给不出理由，需要其他学生的帮忙，解决。

遵循查漏补缺的原则，采取形式多样的练习，以促进学生对面积计算公式的深入理解和灵活运用。

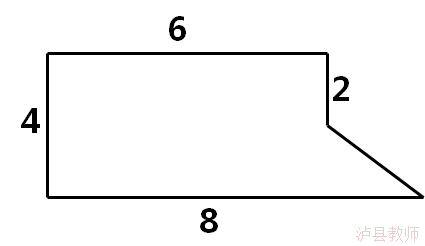
四、提升练习

求组合图形面积

解决问题中学生通过转化的思想利用填补法或分隔法将组合图形转化为简单的多边形，找到解决问题的不同方法。

通过解决问题，拓展练习，启发学生的智慧，培养学生的思维能力，加深学生对平面图形知识的理解。

五、课堂总结

通过本节课复习，你有哪些收获？与大家分享一下吧！

1.学生说出组合图形的面积。

2.学生有可能说出图形面积的推导过程。

通过学生畅谈收获，培养了学生的反思能力，以及他们的概括能力和语言表达能力

六、课后作业：完成练习单

分层练习

七、板书设计

多边形面积的复习

转化

                三角形  

                S=ah÷2

长方形                 平行四边形

S=ab                        s=ah

                                            梯形

                    S=(a+b)h÷2

202311181047105086.pptx