参赛作业设计模板
作业设计团队所在学校(签章):泸县云龙镇学校
作业涉及教科书版本:西师版 年级及册次:六年级下册 | ||||||
作业涉及单元、章节(或主题、任务): 第三单元 | ||||||
作业设计团队教师姓名(不超过5个): 李 勤 | ||||||
单元、章节(或主题、任务)整体性作业设计思路说明(500字以内) 《正比例与反比例》是西师版六年级下册第三单元的内容,本单元是六年级下册重点单元,是除法、分数、比、方程等知识的综合与提升。这一单元依据学习的内容划分为三小节,第一节是学习比例的意义、基本性质,第二节是学习正比例,第三节是学习反比例。 根据本单位学习内容和六年级学生的学习特征,安排了课前作业、课中作业、课后作业。课前作业包括复习与本单元相关的知识及新课预习,意在提高学生的自学能力,促进学生养成良好的学习习惯。课中作业有助于学生巩固理解本节课的知识。课后作业主要运用于课后练习巩固,提高学生运用所学知识解决实际问题的能力及学生创新思维、动手操作能力。 根据不同层次学生的学习发展需要安排基础性作业、发展性作业,难度系数在0.95-0.99。根据本单元学习内容安排 3个课时的随堂练习。每课时作业时间量控制在15至20 分钟左右。课时作业设计注重多样性:书面作业、动手操作等题型均有体现,既注重学生对基础知识和基本技能的掌握,更注重学生基本的思想方法和基本活动经验的积累,培养学生的创新精神和实践能力。 | ||||||
第1课时 | ||||||
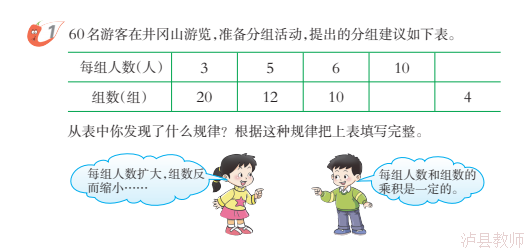
使用时段 | 作业内容 | 作业设计 | 设计意图 | 使用者 | 预计时长 | 预估难度系数 |
课前 | 基础性作业 | 作业一 1、表示两个比( )的式子,叫做比例
| 加深对比例的意义的理解,让学生通过计算比值或者利用比的基本性质来判断能否组成比例。 | 学生 | 1分钟 | 0.99 |
作业二 在14:7=8:4这个比例中,7和8叫做比例的( ),14和4叫做比例的( ) | 学生 | 2分钟 | 0.99 | |||
作业三 在一个比例中,两个内项的积是3,一个外项是,则另一个外项是( )
| 学生 | 2分钟 | 0.96 | |||
发展性作业 | 作业一 1.根据0.6x9=1.8x3,改写成比例正确的是() A .1.8:0.6=3:9 B .1.8:0.6=9:3 C .0.6:9=1.8:3 D .0.6:1.8=9:3
| 学生 | 2分钟 | 0.98 | ||
作业二 如果5A=4B,那么 A : B =( ):( )。
| 学生 | 2分钟
| 0.98 | |||
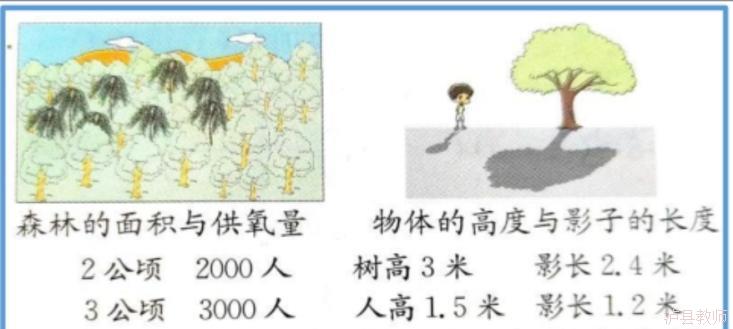
作业三 请根据下两幅图,尝写出几个比例。(至少两个)
| 学生 | 0.96 | ||||
课中 | 基础性作业 | 作业一 能与1/2:1/3组成比例的是()。 A .2:3 B.1/3:1/2 C.1/3:1/4 D.3:2
| 1.通过现实情境,认识比例,能根据比例的意义写出比例。 2.能用不同的方法判断两个比能否组成比例。 | 学生 | 2分钟 | 0.98 |
作业二 在一个比例里,两个外项互为倒数,一个内项是0.5,则另一个内项是( )
| 学生 | 2分钟 | 0.98 | |||
发展性作业 | 作业一 下面各式中,不能与3/5:4组成比例的是( ) A 6:15 B 3:20 C 4/5:16/3 D 0.9:6
| 学生 | 3分钟 | 0.97 | ||
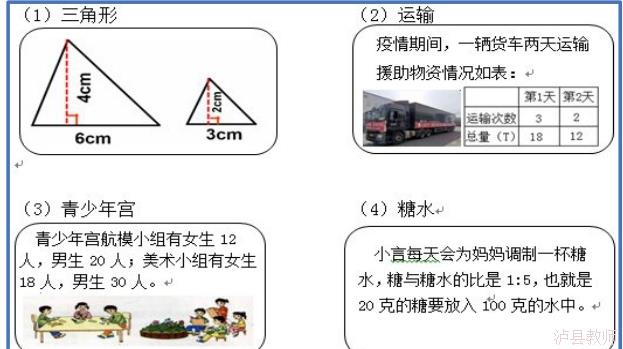
作业二 下面各幅图中相对应的两个量的比能否组成比例?把能组成比例的写出来。(每小题至少写一个)、
| 学生 | 3分钟 | 0.95 | |||
课后 | 基础性作业 | 作业一 为了感谢老客户的支持,中国移动推出了一款优惠活动,每月回馈每个老客户20G流量。爸爸公司有 x 人,共享受了6000G的优惠流量。用比例的知识列式是()。 A .20:1=6000:x B.20:1=x:6000 C . x :6000=20:1 D.x=6000÷20
| 在解决问题的过程中列出含有未知数的比例,并自主探索解比例的方法,会正确解比例,体会解决问题方法的多样性。 | 学生 | 3分钟 | 0.96 |
作业二 奇思和妙想参加"垃圾不落地"环保活动,收集的塑料瓶个数比为5:4,妙想收集了20个塑料瓶,奇思收集的塑料瓶个数是()。 A .16 B.25 C .45 D .36
| 学生 | 2分钟 | 0.97 | |||
作业三 深圳世界之窗的埃菲尔铁塔模型高108米,是按照与原塔高度的比为1:3来建造的,埃菲尔铁塔实际高度是多少米?(用比例的知识解决问题)
| 学生 | 3分钟 | 0.97 | |||
| 发展性作业 | 作业一 海丝商报为第二届的小记者们开展"以物换物闲置互利低碳环保"跳蚤市场活动。小记者们需使用"物物交换"的方式,按一定的比例交换自己所需要的物品。
| 学生 | 2分钟 | 0.98 | |
作业二 一个月黑风高的夜晚,一家珠宝店失窃了。第二天早上,小侦探柯南经过仔细勘察,在案发现场发现了一个犯罪嫌疑人留下的脚印,脚印长28厘米,根据这个脚印,柯南很快判断出了犯罪嫌疑人的身高。请你帮忙算一算,这个犯罪嫌疑人的身高是多少?(科学研究表明:人体身高与脚长的比大约是7:1。)
| 学生 | 4分钟 | 0.95 | |||
第2课时 | |||||||
使用时段 | 作业内容 | 作业设计 | 设计意图 | 使用者 | 预计时长 | 预估难度系数 | |
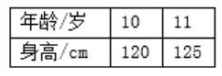
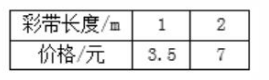
课前 | 基础性作业 | 作业一 下面各表中相对应的两个量的比能否组成比例?如果能,把组成的比例写出来。
| 回顾比例知识 | 学生 | 2分钟 | 0.99 | |
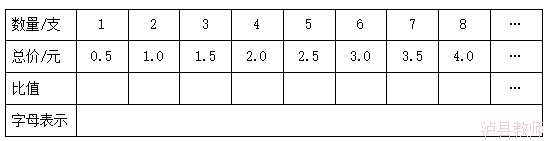
作业二 文具店有一种型号的铅笔,销售的数量与总价的关系如下表。 1.表中有哪两种量? 2.总价是怎样随着数量变化而变化的? | 进一步认识相关联的量 | 学生 | 2分钟 | 0.98 | |||
作业三 1.相对应的总价和数量的比是怎样变化的?比值是多少? 2.如果用字母x和y表示两种相关的量,用k表示它们的比值(一定),正比例关系可以用怎样的式子表示。 | 理解正比例的意义 | 学生 | 4分钟 | 0.98 | |||
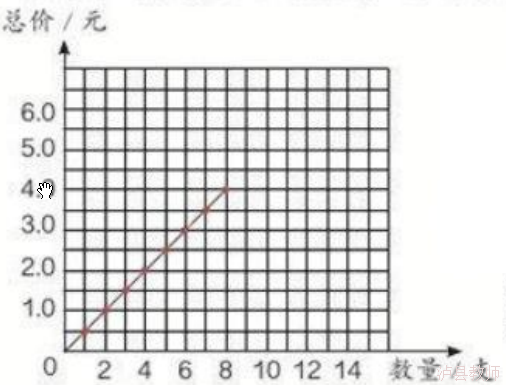
发展性作业 | 作业一 表中的数据用图像(如下图)表示。 1.横轴表示什么?纵轴表示什么? 2.横轴上的数是怎样变化的?纵轴呢? | 培养图象分析能力 | 学生 | 3分钟 | 0.98 | ||
作业二 如何判断两个量是不是成正比例呢? | 理解正比例的实质 | 学生 | 2分钟 | 0.97 | |||
作业三 分别举一个成正比例和一个不成正比例的例子,请你写一写,说一说。 | 感受生活中的正比例 | 学生 | 3分钟 | 0.96 | |||
课中 | 基础性作业 | 作业一 填一填“神舟”十六号飞船太空飞行情况记录如下表。 1.表格中的( )和( )是两种相关联的量,路程随着( )的变化而变化。 2.飞船飞行的路程与时间这两种量中相对应的两个数的比值都是( ),这个比值表示飞船飞行的( )。 3.因为飞船飞行的( )一定,所以飞船飞行的( )和( )成( )比例关系。 | 巩固正⽐例的 意义 | 学生 | 3分钟 | 0.98 | |
作业二 下面每题中的两种量是否成正比例关系,并说明理由。 1.苹果的单价一定,苹果的总价与数量 2.汽车行驶的速度一定,行驶的时间与路程 3.人的年龄与身高 4.正方形的边长与周长
| 加深对正⽐例关系本质的理解。 | 学生 | 2分钟 | 0.98 | |||
作业三 1.正方形的面积和边长( )。 A.不成比例关系 B.成正比例关系 C.无法确定 2.能表示x和y成正比例关系的式子是( ) A. x +y =6 B. x÷y =10 C. x-y=4 3.下面的式子中,x与y成正比例关系的是( )。(x、y均不为0) A. x+3=y B. x-5=y C.x÷5=y
| 通过变式进一步理解正比例的意义 | 学生 | 5分钟 | 0.97 | |||
发展性作业 | 作业一 已知某三角形的底边长,根据下表中该三角形面积与底边上的高相对应的数据。判断它们是不是成正比例,并说明理由。
| 巩固正比例的意义 | 学生 | 3分钟 | 0.96 | ||
作业二 据说,埃及的金字塔修成1000多年后,没有人能够准确的测出它的高度。人们尝试过很多方法,但都没有成功。古希腊人泰勒斯用数学方法测量出了金字塔的高度。泰勒斯站在金字塔前,让别人测量他影子的长度,当他影子的长度与他的身高完全相等时,他立刻在金字塔的投影处做出一记号,测量金字塔影子的长度,这样,就得到了金字塔的高度。 想一想,说一说,泰勒斯测量金字塔高度的道理是什么?如果身高和影长的比不是1:1时,你还能测量出金字塔的高度吗?
| 解决生活中的实际问题 | 学生 | 4分钟 | 0.95 | |||
课后 | 基础性作业 | 作业一 填空题。 圆的周长和半径成( )比例。 长方形的长一定,( )和( )成正比例。 工作效率一定,( )和( )成正比例。 如果x=9y(xy≠0),那么y与x成( )比例。
| 作用正比例的意义 | 学生 | 2分钟 | 0.98 | |
作业二 判断下面两种量是否成正比例关系。 1.每人植树棵数一定,参加植树的人数和植树总棵树。 2.人的体重与人的年龄。 3.每小时织布长度一定,织布总长度和时间。 4.圆柱的高一定,体积和底面半径。 5.圆的面积和半径。
| 理解正比例的意义和本质 | 学生 | 2分钟 | 0.98 | |||
|
| 作业三 已知 x和 y成正⽐例关系,请把表格填写完整。 | 加深理解正比例意义 | 学生 | 2分钟 | 0.97 | |
发展性作业 | 作业一 同⼀时间、同⼀地点测得树⾼和影⻓的数据如下表: 1.树⾼ 8⽶时,影⻓多少⽶? 2.影⻓ 5.6⽶时,树⾼多少⽶?
| 巩固正比例意义 | 学生 | 两分钟 | 0.97 | ||
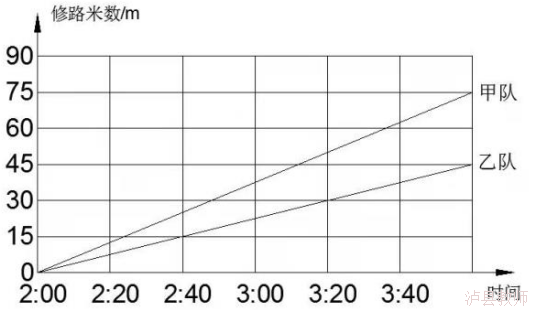
作业二 下⾯是两个⼯程队某⽇下午 2:00开始修路情况,请计算每个队到下午 4:50各修了多少⽶路。
| 利用正比例图象解决问题 | 学生 | 3分钟 | 0.96 | |||
作业三 利用所学知识想一想怎样测量学校旗杆的高度。先设计实施方案,再和同学一起实践。
| 解决生活中的正比例问题 | 学生 | 8分钟 | 0.95 | |||
第3课时 | ||||||
使用时段 | 作业内容 | 作业设计 | 设计意图 | 使用者 | 预计时长 | 预估难度系数 |
课前 | 基础性作业 | 作业一 1.仔细阅读书48页例1。 通过表格,我知道( )是反比例的量, ( )是反比例关系。 我总结的反比例的三个要素( )。
| 前置性作业,让学生学会预习,在预习中独立思考,理解反比例的意义,为新授课打下基础。 | 学生 | 5分钟 | 0.99 |
发展性作业 | 作业一 把相同体积的水倒入底面积不同的量杯中,(如图所示)杯子的底面积与水的高度的变化情况如下表: 杯子底面积(cm²)1015203060 水的高度(cm)302015105 体积 算式 1.表中有哪两种量?它们是不是相关联的量? 2.你能计算出水的体积吗?并比较积的大小。 3.观察这三种量的变化规律,你发现了什么? 我的例子 。 | 通过表格形式的呈现,找出相关联的量,过程中培养学生分析数据的能力, | 学生 | 5分钟 | 0.97 | |
课中 | 基础性作业 | 作业一 相对应的两个数的乘积是( )。这个乘积表示( ),用关系式表示是( )。 | 理解反比例意义 | 学生 | 2分钟 | 0.99 |
作业二 ( )1.已知: a+b=8,b和8。 ( )2.笑笑的身高与体重。 ( )3.做游戏的人数一定,每组的人数与组数。 ( )4.一本书,看了的页数与未看的页数。 ( )5.长方形的面积一定,长方形的长和宽。 | 根据反比例意义来判断两个量是否成反比例 | 学生 | 3分钟 | 0.98 | ||
作业三 学校食堂要给餐具消毒,要用200mL消毒液配成消毒水,如果消毒液与水的体积比是1:180,那么应加入水( )mL。 A.180 B.360 C.36000 D.18000
| 让学生灵活运用正、反比例的意义解决问题。 | 学生 | 2分钟 | 0.97 | ||
发展性作业 | 作业一 一个平行四边形的面积是24平方厘米,用a和h表示它的底和高。a与h成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
| 巩固对反比例关系的本质理解。 | 学生 | 5分钟 | 0.95 | |
课后 | 基础性作业 | 作业一
①题目中两种相关联的量是( )和( )。 ②根据“买同样的236套”,可知每套吉祥物的( )一定,也就是说买吉样物的总价与数量的( ) 一定,所以这两种相关联的量成( ) 比例关系。 ③用比例知识解答,设花费x元,列式: | 考查学生结合生活实际,用比例知识来解答,让学生从量与量之间的关系思考,培养代数思维,体会函数思想。 | 学生 | 4分钟 | 0.97 |
作业二 云龙学校组织学生到泸县宋代石刻博物馆参观,不同的交通工具的速度和行驶所需时间如下。你从表中发现了什么? 自行车公交车轿车速度(千米/小时)153060时间(时)31.50.5
我的发现
| 解反比例实例,让学生积极参加课外实践活动,了解我县丰富的历史文化,并培养学生的调查、分析数据的能力 | 学生 | 4分钟 | 0.97 | ||
发展性作业 | 作业一
| 考查学生能够正确找出两种相关联的量,判 断它们成哪种比例,然后根据正比例或反比例的意义列出方程。
| 学生 |
6分钟 | 0.96 | |
作业二
| 加深学生对正、反比例概念的理解,也为中学数学、物理、化学等学科应用比例知识解决一些问题做好准备。 | 学生 | 6分钟 | 0.95 | ||







账号+密码登录
手机+密码登录
微信扫码登录
还没有账号?
立即注册