《平行四边形的面积》教案　 程丽霖

《平行四边形的面积》教案

泸县实验学校   程丽霖

【教学内容】

教科书第79页例1、，课堂活动第1题。

【教学目标】

1. 利用方格纸或割补等方法，探索并掌握平行四边形的面积计算公式，会用这个公式计算图形面

2.能主动应用原来掌握的相关知识探索新知识，在主动探索知识的过程中获得成功体验

3.在探索知识的过程中培养学生的合作意识和多向思维的能力。

【教学准备】

教具：平行四边形卡纸、课件。

学具：平行四边形卡纸、剪刀、三角板、小棒等学具。

【教学过程】

一、创设情景

师：孩子们，今天老师请来了两位朋友，你们认识吗？我们一起来听听阿凡提的故事吧。请听——

巴依老爷家有很大一片菜地，他想找人给菜地翻土，却又不想给工钱。于是他拿出了4根竹竿，其中2根长8米（课件出示），两根长5米（课件出示）,对阿凡提说：“阿凡提，我和你打个赌，你用四根竹竿首尾相连去围一块菜地（课件出示），如果能在一个时辰内把所围成的菜地翻一遍土，我就给你一只羊。否则你除了白白给我翻土以外，还要赔我一只羊。”

巴依老爷心里盘算着（课件出示长方形）：阿凡提一个时辰内最多翻32m²的地，用这4根竹竿去围成一个长方形地，在一个时辰内是绝对翻不完的，阿凡提肯定输定了。

师：前面我们已经学过长方形。谁来说说长方形的面积公式是什么？

生：长×宽。

板书：长方形的面积=长×宽。

师：还记得长方形的面积公式当时是怎样验证的吗？

生：把长方形用面积单位摆满。一共有8×5=40个面积单位。一排有8个这样的面积单位，长是8；有5排，宽是5。就用8×5得到40m²。

师：我们就是根据面积单位的个数与长、宽之间的关系就验证出长方形的面积公式。

阿凡提想：我把它拼成面积为32m²或小于32m²的图形，就赢了。

师：假如你是阿凡提，你会怎么想？阿凡提就拼出了一个这样的图形，叫什么呢？（平行四边形），那这个平行四边形的面积是多少呢？符合他的想法吗？

根据老师提供的这几个数据，请你大胆猜一猜平行四边形的面积是几乘几?

生：8×4=32（m²）或8×5=40（m²）（板书）

师：有的孩子认为平行四边形的面积是底乘高，有的认为是邻边相乘，那这只是你们的猜想，怎样验证呢？今天，我们就一起来探究平行四边形的面积。（板书课题）

二、探究新知

师： 孩子们，知道吗，很多伟大的发现都是从猜想开始的。我们还得寻找方法去验证我们的猜想，你们有什么办法探究平行四边形的面积吗？

生：数方格、剪拼成长方形。

师：接下来，咱们就分小组，利用老师给大家提供的学具，准备开启验证之旅。在开始之前，先请一名同学大声地朗读合作要求：

4人为一组，选择适当的工具，通过数一数、剪一剪、拼一拼等方法，探究平行四边形面积的计算方法，并完成学习单。

小组汇报。

1、数格子的方法

师：这个小组是用什么方法来验证的？（数格子）把平行四边形放在格子图中，出现了半格，他是怎么做的呢？

师：数出面积是32m²，底是8m，高是4m，数出来的面积正好是底与高的积。还有不同的数法吗？

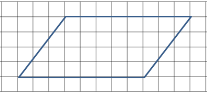
师：说的真好，刚才我们借助方格纸度量出一个平行四边形的面积，发现平行四边形的面积=底×高。老师再给你们两个平行四边形，你们能快速数出它们的面积吗？

生：不能。太麻烦了。

师：是的，如果没有方格纸怎么办呢？同学们还有什么办法呢？（小组汇报）

师：你们听懂这个小组的做法了吗？他们组其实是先剪、再拼，最后把平行四边形变成了什么图形？（长方形）这个剪拼法有点意思。老师有个问题想问问你，我们不是在探究平行四边形的面积吗？你为什么要把它变成长方形呢？

师：老师听懂你的意思了，你是想把我们没有学过的知识变成我们学过的知识，孩子们，其实他的这个操作过程，用到了数学上很重要的一个思想，叫做：转化思想，把我们不会算面积的平行四边形转化成了会算的长方形。（板书转化，箭头）老师还想问问你：转化成长方形之后，面积变了吗？

生：没有改变。

师：为什么面积没有变？

学生回答。

师：什么没有变？（面积），什么变了？（形状）

师：为什么平行四边形的两条斜边一定能拼合？

生：两条斜边互相平行且相等，所以平移后，可以重合。

师：同学们非常善于思考和表达，掌声送给他们。

师：我们可以沿着顶点作下来的高剪，还有其他剪法吗？（学生展示）你是沿着哪里剪的？（两条平行线间的高）

师：谢谢你的分享。刚才这两个小组的剪拼方法有什么共同点？（都是沿着高剪）你们为什么会沿着高剪？ 

生：长方形有4个直角，只有沿着高剪才能剪出直角。不能。

师：我们沿着高剪，就是为了创造什么？（直角）。长方形4个角都是直角，把平行四边形沿着高剪，就可以拼成长方形。我们一起来看看，如果不沿着高剪，这样剪，拼成的是一个什么图形？（平行四边形）。

师：换一个平行四边形，用剪拼的方法还能拼成长方形吗？我们来看一看（动画演示）抽生上台在数学画板上移动。

师：其实啊，我们的剪拼方法还有很多，我们来欣赏一下（希沃数学画板变换二、变换三）。无论是什么样的平行四边形，都可以转化成和它面积相等的长方形。咱们就是利用的割补法实现这样的转化。

师：拼成的长方形的长和宽与平行四边形的底和高有什么关系？原来平行四边的底就等于长方形的长（板书箭头），原来平行四边形的高就等于长方形的宽。刚才我们还知道了长方形的面积=平行四边形的面积。因为长方形的面积=长×宽，所以平行四边形的面积=底×高。

师：在数学上，我们用S表示平行四边形的面积，a表示平行四边形的底，h表示平行四边形的高，那么平行四边形的面积公式可以表示为：S=a×h。

师：割补法在我国古代数学著作中被称为“出入相补，以盈补虚”，我们一起来看看吧。（播放视频）

师：出入相补，以盈补虚的方法不但可以用在求平行四边形的面积中，在之后的学习中我们也会用到哦。

师：现在我们回归开始的问题，阿凡提能不能赢？

生：平行四边形的面积：8×4=32（m²）答：阿凡提能赢。

师：如果你是阿凡提，你会怎么围平行四边形呢？你有什么办法让平行四边形的面积尽可能的小呢？

学生说一说，再让学生拼。

（展示活动的平行四边形）通过压缩，让学生知道面积和高的长短有关。

拖动，高不断变化，学生口算面积。

师：请同学们仔细观察，在拖动过程中，什么变了，什么没变？

生：高边了，面积变了。

生：底没变，周长没变，邻边没变。

师：平行四边形的面积只跟底和高有关，跟周长、邻边无关，在底不变的前提下，平行四边形的高越短，面积就越小。

师：所以阿凡提想要赢，只要让平行四边形的高尽可能短就行了。

三、巩固新知

师：接下来我们来做一些练习。

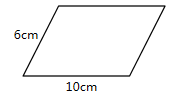
1、求出下面平行四边形的面积。（单位：厘米）

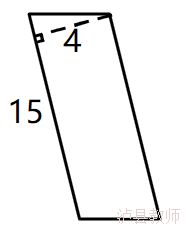
师：第一题，谁来说说怎么列式？

生：15×4=60（cm²）

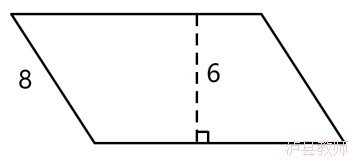
第二题呢？怎么列式？

生：高对应的底不是8cm。

师：老师知道了，要算平行四边形的面积要知道它的底和高，还得是（对应）的。（板书：对应）。我们看一看，如果沿着这条高剪的话，把它平移过来，高是6cm，底是8cm吗？（不是）能用8×6来计算吗？（不能）那要想求这个平行四边形的面积，还要知道什么数据呢？谁来说一说算式？

生：12×6=72（cm²）或8×9=72（cm²）

师：孩子们，其实咱们做题，重要的不是做了多少道题，重要的是每道题对你们有什么收获？

通过这道题，你有什么想提醒大家注意的？

2、羊村新办了开心农场，三个小朋友各自分得了一块地。但是，他们都有点不开心，都认为对方的土地面积更大。孩子们，我们来帮他们比一比，谁的面积比较大？

学生说一说。

师：现在来比一比呢？（把三个平行四边形底重叠。）

生：三个平行四边形的底重合，说明它们的底相等。高就是两条平行线间的距离，也是相等的。所以面积也相等。（画高）

师：接着用几何画板演示，它们的面积呢？得出结论：等底等高的平行四边形面积相等。

像这样，在一组平行线之间，等底等高的平行四边形有多少个？（无数个）

师：通过这节课的学习你有什么收获？

拓展练习：3. 下面平行四边形的高为8cm，求面积。

四、课堂小结

   师：通过今天的学习，你有什么收获？

师：孩子们，这节课我们研究了平行四边形的面积，我们开始是通过大胆猜想，小心验证，把不会算的平行四边形转化成会算的长方形，最后得出结论，解决了问题。这个转化的数学思想非常重要。在以后研究三角形、梯形、圆形的时候，我们都可以用今天学到的转化的思想去研究。今天这节课我们就学到这里，下课。

《平行四边形的面积》教案

《平行四边形的面积5.30》

https://13.r302.cc/ykG5v1Z?platform=enpc&channel=copylink

点击链接直接预览课件